数学这门学科，是以人们的社会生活需要以及客观现象为研究对象，是人类理解自然、征服自然的有力武器。而地理学是一门兼有自然科学和人文社会科学的综合性学科。这在一定程度上决定了地理与“一切自然科学的基础”的数学之间具有密切的联系。

一、早期数学于地理的应用

埃拉托色尼(约公元前274-前195)是最早把地理学作为独立学科进行研究的学者，所以也被称为“地理学之父“。在他生活时期，有人认为地球是方的、有人认为是扁的，他始终坚持认为地球是个球体，并尝测量地球这个球体大圆的周长长度。

由于太阳离地球非常远，假设在同一个时间太阳照射到地球的光线是彼此平行的。但是光线的方向和地面是有角度的，角度会随时间的变化而变化。经过几年的观察和统计，他发现太阳垂直于地面照射的地点是存在一个区域范围的，也就是我们现在说的南北回归线。

太阳的垂直照射点每年都在南北回归线之间来回移动。比如在每年北半球的夏至时，太阳会垂直照射到北回归线上，夏至之后，太阳照射点就会往南移动了。他发现尼罗河东岸的塞恩纳就在太阳直射最北的边界上，每年到了夏至那一天的下午，这里无论建筑还是人的影子，都会缩成一个点，太阳光甚至可以直直照到井底，而在塞恩纳正北方向5千希腊里的亚历山大城，夏至这天，太阳照射方向与垂直方向的夹角约为周角的50 分之一，也就是大约7.2°。

这个角度是埃拉托色尼通过测量亚历山大城的高塔和塔影计算出来的。对于地球这个球体，我们把经过塞恩纳和亚历山大城的这个球大圆单独拿出来分析。夏至这天，太阳的光线是垂直于塞恩纳的，而平行的光线照射到亚历山大城，就有了50分之一周角的角度，根据平行线之间的角度关系，塞恩纳到亚历山大城之间这段弧所对的圆心角就是50分之一周角的度数，所以这段距离为5千希腊里的弧就是整个球大圆轴承的50分之一了，于是地球球大圆的周长大约就是25万希腊里了。当时的1希腊里约为现在的157.5米，所以埃拉托色尼测出的地球周长就约为3.9万公里。

我们利用现代科技精确测量的地球周长是4万公里左右。可以说，埃拉托色尼测量的结果，在他所在的那个时代已经非常精准了。在这之后，埃拉托色尼还测量了赤道的长度、回归线与北极圈的距离等等，还大致计算出了太阳、地球和月亮之间的距离。

通过这个故事我们了解到，几何学知识也是可以用到地球这个庞然大物身上的，所以说数学”大“有用处。

接下来我们主要从数学思想、数学工具上来看看数学在地理中的应用。

二、地理中的数学思想

1、 数形结合思想。

根据数据与图像之间存在的对应关系，通过相互转化的形式来表达两者之间关系的思想就是数形结合思想。地理中数形结合思想能够以数字和图像相结合的的直观形式呈现地理现象的的变化和规律，使复杂的地理现象简单化。

如运用在气温降水类型分异图中，会比表格、数字资料给出更明确的气候概念分布。同时给出气候要素在地域上变化的连续性，反映出地理条件的影响，综合反应一系列气候要素或指标的区域分布和相互关系。

数形结合思想在地理的地震波传播速度分异，雪线高度差异，全球气候演变周期、城市化进程、世界水资源分布等也有应用。

（气温降水分布图）

2、分类讨论思想

分类讨论是将要研究的对象按照一定的标准划分为若干不同的情形，然后再逐类进行研究和求解的一种数学思想。

我国西部海拔高，东部海拔低。地势呈三级阶梯状逐级下降，依据海拔高度地势可划分为第一阶梯、第二阶梯、第三阶梯。

第一阶梯面积约占中国面积四分之一，包括柴达木盆地、青藏高原，位于昆仑山、祁连山之南、横断山脉以西，喜马拉雅以北，平均海拔4000米以上，四周被高山围绕。

第二阶梯位于我国中部及北部，包含了内蒙古高原、黄土高原、云贵高原、准噶尔盆地、四川盆地、塔里木盆地六大部分，平均海拔2000-1000米之间。

第三级阶梯位于我国东部。包含东北平原、华北平原、长江中下游平原、辽东丘陵、山东丘陵、东南丘陵六部分，平均海拔在500米以下。

从高冷的雪山到炎热的沙漠，从寂寥的荒野到茫茫的林海，我国地理环境丰富多样。通过三级阶梯的划分，把我国复杂的地理环境总体上分为三大板块，更加利于管理和规划，是数学分类讨论思想在地理中的一大应用。

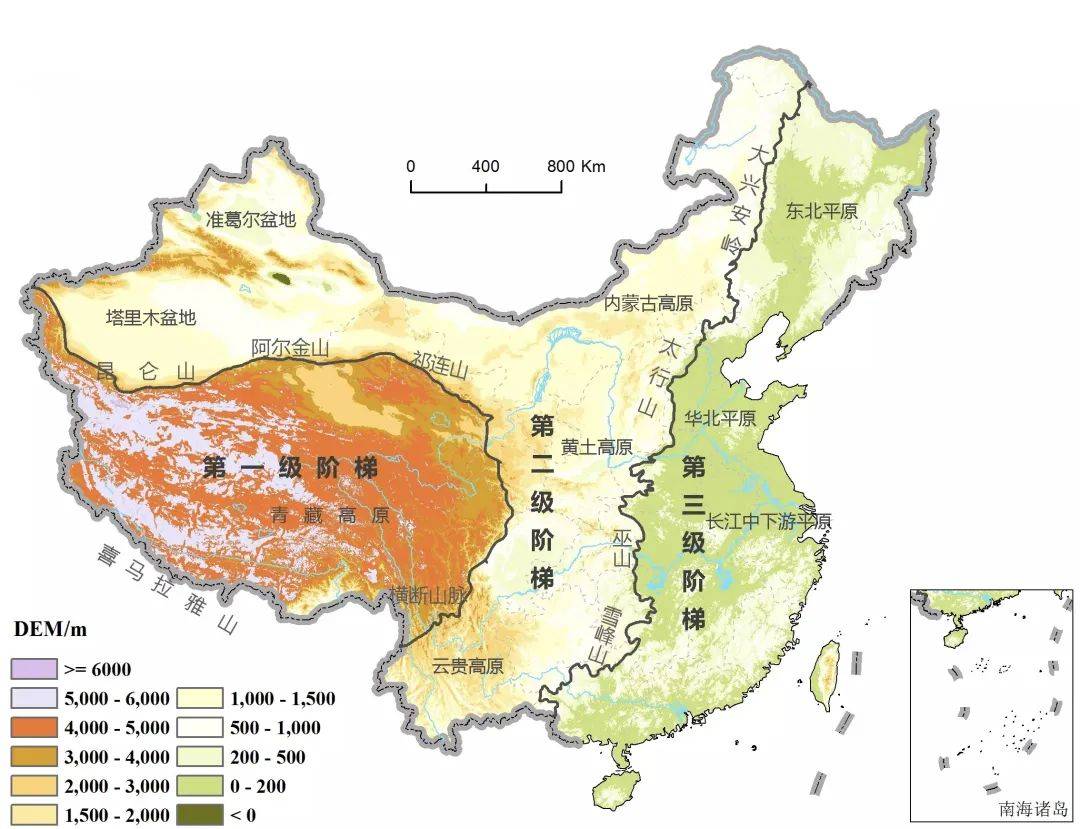
（中国的三级阶梯）

三、数学工具在地理中的运用

地理与数学工具的交叉融合，常用的数学工具有坐标系、数学图形等。

1、 坐标系。

经纬度其实就是为地球搭建的坐标系、地图上的辅助线。维度是地球的纵坐标，是地球面上一点与地球球心的连线和地球赤道面所成的线面角。经度是地球的横坐标，是地球面上一点与两级的连线与0度经线所在平面的夹角。这样的虚拟线，让我们有了定位任意地点的能力。同时，在研究城市内部空间结构时，研究地租水平和距城市中心距离间的关系借助平面直角坐标系就会简单很多。

2、数学图形

数学图形按照内容分类可以分为函数图形、几何图形，按照形态分类可以分为平面图形和空间图形。

褶皱是在地壳运动作用下岩层发生波浪型状的塑性形变。褶皱的基本单位为褶曲，一个褶曲包括一个背斜和一个向斜。背斜岩层一般为向上拱起，向斜岩层一般为向下弯曲。此时，在描述褶曲这一概念时，可以借用y=sinx的正弦曲线来进形形象解释。将褶皱的一个褶曲理解为正弦曲线的一个周期（2π） 。将背斜、向斜分别对应正弦曲线的前、后半个周期（π） 。

除此之外，利用三角函数曲线解释太阳直射点的回归运动轨迹。将大洲轮简化为几何图形去识记大洲、洋流、气候类型等。以及运用扇形图、饼图、柱状图等统计图进行概念理解和数值表示。都是数学图形在地理中的应用。

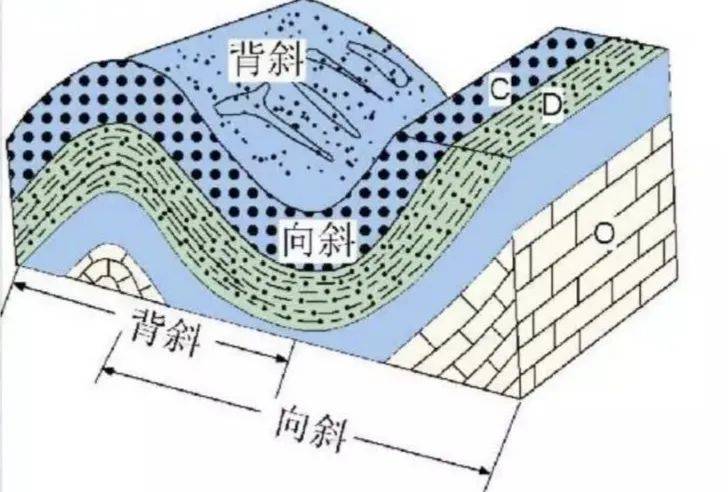
（褶皱的基本形态）

四、GIS

GIS（地理信息系统）是一个集成了地理学和数学技术的重要工具，它可以帮助地理学家在地图上可视化和分析数据。

空间优化：GIS中常常需要进行网络分析、路径规划、区域划分等优化操作。这些优化算法基于高等数学中的最优化理论和线性代数知识。

空间插值：GIS中常常需要对缺失的数据进行插值操作，如地形高度、土地利用、气象数据等等。这些插值算法基于高等数学中的插值理论和微积分知识。

除此之外，数学中的统计学和空间分布技术可以帮助地理学家对人口、资源和地形进行分析和预测。